Ingenieurbiologie
- Genie Biologique, Nr. 4, Dezember 2001
Ermittlung von charakteristischen Strömungsparametern in verzweigten
und unverzweigten Gerinnen mit dem Flachwassermodell Hydro2de
Détermination des paramètres caractéristiques du courant
dans des lits ramifiés et non ramifiés avec le modèle
en eaux peu profondes Hydro2de
Cornel Beffa und Joachim Hürlimann
Zusammenfassung
Es werden zwei Anwendungen des Flachwassermodelles
Hydro2de
zur Ermittlung charakteristischer Strömungsparameter präsentiert.
Die Vergleiche zwischen beobachteten und modellierten Wassertiefen zeigen
eine gute Übereinstimmung, sowohl in verzweigten als auch in unverzweigten
Gerinnen. Bedingung dafür ist, dass die zur Verfügung stehenden
Daten eine ausreichende Auflösung der relevanten Sohlenstrukturen
ermöglichen. Die freien Parameter des Modelles lassen sich direkt
aus Naturgrössen herleiten; eine Kalibrierung ist somit nicht erforderlich.
Hydro2de
erweist sich innerhalb seines Gültigkeitsbereiches als sehr vielseitig
und effizient einsetzbares Instrument zur gewässerökologischen
Beurteilung von Gerinnen. Richtig eingesetzt, vermag es die Planung und
Optimierung von Gestaltungsmassnahmen an Gewässern wirkungsvoll zu
unterstützen.
Schlüsselwörter: Modellierung,
Fliessgewässer, Strömungssimulation, Flachwassergleichung, Restwasser
Résumé
Deux applications du modèle en eaux
peu profondes Hydro2de permettant de déterminer des paramètres
caractèristiques du courant sont présentés. La comparaison
entre les hauteurs d'eau observées et modélisées montre
une bonne concordance, autant pour les lits ramifiés que pour les
lits non ramifiés. Il est toutefois nécessaire que les données
disponible permettant une définition suffisante des structures importantes
du lit. Les paramètres libres du modèle étant obtenus
directement à partir des données naturelles, un calibrage
n'est pas nécessaire. A l'intérieur de son domaine de validité,
Hydro2de apparait comme un instrument offrant de nombreuses possibilités
et d'une grande efficacité pour l'evaluation écologique des
cours d'eau. Correctement utilisé, il facilite et améliore
la planification et l'optimisation des mesures d'aménagement des
cours d'eau.
Mots clés: Modélisation,
cours d'eau, simulation du courant, équation des eaux peu profondes,
débit résiduel
Einleitung
Fliessgewässer haben eine wichtige
Funktion als Lebensraum für Wassertiere und Pflanzen und als Erholungsraum
für den Menschen. Während früher der Hochwasserschutz im
Mittelpunkt von flussbaulischen Massnahmen stand, sollen heute Hochwasserschutz
und Ökologie keine Widersprüche mehr darstellen. Dies ist möglich,
wenn dem Gewässer der nötige Raum gewährt wird (BWG 2000).
Die Einhaltung von angemessenen Restwassermengen soll im weiteren dafür
Gewähr bieten, dass auch bei der Wasserkraftnutzung die übrigen
Gewässerfunktionen berücksichtigt werden (BUWAL 2000).
Der Nachweis und die Optimierung der Abflusskapazität
eines prismatischen Trapezgerinnes ist mit wenig Aufwand möglich (Vischer
& Huber 1993). Die ökologische Beurteilung eines solchen Gerinnes
und die Festlegung von angemessenen Restwassermengen ist hingegen wesentlich
anspruchsvoller. Für ein Gerinne mit variabler Geometrie und Rauheit
(alternierende Bänke, verzweigte Gerinne, bestockte Flächen etc.)
sind diese Nachweise noch schwieriger zu erbringen. Ohne ausreichende Kenntnis
der Strömungsparameter ist an eine Optimierung der Gewässerfunktionen
jedoch nicht zu denken. Auch lassen sich nur bei sorgfältiger Planung
die vorhandenen Mittel effizient einsetzen.
Im vorliegenden Beitrag wird ein zweidimensionales
Berechnungsmodell vorgestellt, das sich für eine Vielzahl von Anwendungen
als nützliches Arbeitsinstrument erwiesen hat. Das Modell erlaubt
die Bestimmung der wichtigsten Strömungsparameter bei Hoch- und Niedrigwasserabflüssen
sowohl in steilen, flachen, konkaven und gegliederten Gerinnen.
Das Flachwassermodell Hydro2de
Abflüsse in offenen Gerinnen besitzen
in der Regel eine - im Verhältnis zur Gerinnnebreite -, geringe Wassertiefe.
Aufgrund der hydrostatischen Druckverteilung lassen sich solche Strömungen
mittels der Flachwassergleichungen beschreiben (z.B. Liggett 1994). Das
numerische Modell Hydro2de basiert auf eben diesen (tiefengemittelten)
Flachwassergleichungen und verwendet zu deren Lösung ein zellenzentriertes
Finite-Volumen Verfahren (Beffa 1994, Beffa & Connell 2001). Das Modell
berücksichtigt dabei Energieverluste durch Sohlenrauheiten (wahlweise
mit dem logarithmischen Fliessgesetz oder mit dem Ansatz von Manning-Strickler
(Strickler 1923)) und Bewuchs (Ansatz von Lindner (1982)). Der Einfluss
von turbulenten Spannungen auf das Strömungsfeld wird durch ein Null-Gleichungsmodell
parametrisiert (Rodi 1984).
Hydro2de hat sich in einer Vielzahl von Anwendungen als sehr
robustes numerisches Werkzeug erwiesen. Aufgrund seiner Stabilität
auch bei gemischt unter- und überkritischen Abflüssen sind Strömungssimulationen
in verzweigten Gerinnen (Beffa 1996) und bei Ausuferungen in weiten Vorlandflächen
(Connell et al. 2001) möglich. Durch die hohe Stabilität des
Lösungsverfahrens und der hohen Rechenleistung moderner PC´s
können sehr hoch auflösende Berechnungsgitter mit mehreren hunderttausend
Gitterzellen eingesetzt werden. Speziell entwickelte Module für das
Prä- und Postprocessing dienen zur effizienten Generierung und Visualisierung
von grossen Berechnungsgittern aus vorhandenen Geländeinformationen.
Hydro2de
basiert auf einem einheitlichen Raster, was die Anbindung an GIS Programme
vereinfacht. Das Programm bietet zudem die Möglichkeit, innerhalb
von GIS erstellte Raster zu lesen und die Resultate im gleichen Format
zu schreiben.
Im folgenden sollen zwei Anwendungen von kleinerem Umfang gezeigt werden,
welche sich zur Illustration der Möglichkeiten des Modelles gut eignen.
Anwendung 1 beschreibt den Modelleinsatz an einem verzweigten Gerinne,
welches durch eine grosse morphologische Struktur geprägt wird. In
Anwendung 2 wird der Einsatz des Modelles in einem verbauten Gerinne gezeigt,
wo es um die Festlegung von angemessenen Restwassermengen geht.
Anwendung 1: Verzweigtes Gerinne
Der North-Ashburton River (Neuseeland)
fliesst auf einem alluvialen Gerinnebett über die Canterbury Plains
von den Südalpen ins Meer (Abbildung 1). Im betrachteten Abschnitt
beträgt das mittlere Gefälle 1% und die gesamte Gerinnebreite
liegt bei rund 100 m. Aufgrund der zahlreichen Gerinneäste ist die
Strömungsvielfalt sehr hoch. Stromschnellen mit kritischem oder überkritischem
Abfluss wechseln ab mit Abschnitten von reduzierter Fliessgeschwindigkeit.
Das Gewässer hat Bedeutung als Fischhabitat und wird für Bewässerungszwecke
genutzt. Probleme bereiten die abnehmende Abflusskapazität als Folge
der Sohlenauflandungen.

Abbildung 1: North-Ashburton River: Ansicht
des Modellperimeters von der Thompson Track Bridge mit Blick gegen die
Fliessrichtung. (Foto: G. Smart)
Die ausgeführte Untersuchung dient primär
der Fragestellung, wie weit sich die grosse Variabilität der Strömungsparameter
in einem numerischen Modell nachbilden lässt. Dazu ist in einem Abschnitt
von 500 m Länge die Sohlentopographie detailliert vermessen worden.
Für die trockenen Flächen geschieht dies mittels photogrammetrischer
Auswertung mit einer Höhengenauigkeit von 5 cm. Die benetzten Flächen
werden terrestrisch vermessen, wobei gleichzeitig die Wassertiefe notiert
wird (Abbildung 2a). Ein Zweierteam benötigt für die ergänzenden
Feldaufnahmen rund drei Tage.
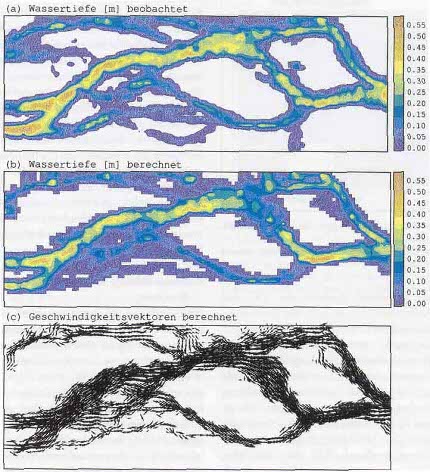
Abbildung 2: North-Ashburton River:
Wassertiefen und Fliessgeschwindigkeiten für den Modellperimeter (Länge:
240 m, Breite: 86 m) bei einem Abfluss von 3.5 m3/s.
Damit kann die Modellierung beginnen: Aus
den Einzelmessungen wird mittels Triangulation ein digitales Terrainmodell
(DTM) der Sohlentopographie erstellt. Daraus lässt sich im nächsten
Schritt ein Rechteckraster generieren, welcher als Grundlage für die
hydrodynamische Berechnung dient. Der Rauheitsparameter kann mit der Stricklerformel
(Strickler 1923) aus dem mittleren Korndurchmessers des Sohlenmaterials
abgeleitet werden . Nach Zuordnung von geeigneten Randbedingungen am Zu-
und Abflussrand lassen sich die Strömungssimulationen durchführen.
Insgesamt erzielen die berechneten Wassertiefen
in Abbildung 2b eine gute Übereinstimmung mit den Naturbeobachtungen.
Bei näherer Betrachtung sind aber auch Abweichungen - vor allem in
den seichten Zonen -, festzustellen. Die Modellgenauigkeit hat ihre Grenzen
offensichtlich dort, wo feine Sohlenstrukturen nicht mehr in der nötigen
Schärfe abgebildet werden. Für ökologische Bewertungen interessiert
die statistische Verteilung der Strömungsparameter, beispielsweise
die Summenhäufigkeit der Wassertiefen in Abbildung 3. Die sehr gute
Übereinstimmung zwischen Natur und Modell ist dabei ohne Kalibrierung
erzielt worden. Damit erfüllt das Modell die Voraussetzungen, um als
Prognosewerkzeug zu dienen (Cunge 1998). Die Darstellung der tiefengemittelten
Fliessgeschwindigkeit in der gleichen Abbildung soll zeigen, welche Möglichkeiten
die Modellrechnung im Vergleich zu Feldaufnahmen bietet. Das verifizierte
Modell erlaubt die Ausgabe der Strömungsparameter für beliebige
Abflüsse quasi "auf Knopfdruck". Im Vergleich zu den zeitintensiven
Feldaufnahmen stellt dies ein beträchtliches Sparpotenzial dar.
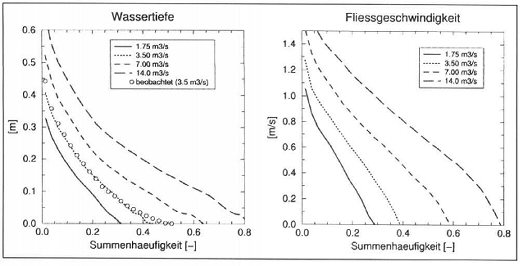
Abbildung 3: North-Ashburton River:
Berechnete Summenhäufigkeit von Wassertiefe und tiefengemittelter
Fliessgeschwindigkeit bei verschiedenen Abflussmengen.
| Modellänge / -breite |
240 / 86 m
|
| Zellengrösse |
2 ´ 2 m
|
| Anzahl Zellen |
5160
|
| k-Strickler-Wert |
30 m1/3/s
|
| Zuflussrand |
Normalabfluss
|
| Wegflussrand |
kritischer Abfluss
|
| Berechnungszeit pro Run (PIII, 866 MHz) |
45 s
|
Tabelle 1 - Angaben zum Modell "North-Ashburton
River"
Anwendung 2: Unverzweigtes Gerinne
Die Sarner Aa (Kanton Obwalden) verbindet
Sarner- und Alpnachersee. Durch die Stauhaltung Wichelsee beim Kraftwerk
Sarneraa wird dem Gewässer auf einer Länge von 2 km bis zu 12
m
3/s des vorhandenen Wassers entzogen. Im Rahmen der Neukonzessionierung
stellt sich die Frage nach den Abflussverhältnissen entlang der Restwasserstrecke
sowie nach den angemessenen Restwassermengen. Die Morphologie der Restwasserstrecke
ist geprägt durch eine Sohlenpflästerung, welche bei der Korrektion
der Sarner Aa als Erosionsschutz eingebracht wurde, und das beinahe vollständige
Fehlen der Kiesfraktion (Abbildung 4). Die Aufgabe besteht nun darin, die
hydraulischen Grundlagen bereitzustellen, damit die Organismendurchgängigkeit
beurteilt werden kann.

Abbildung 4: Sarner Aa: Ansicht des
Gerinnes unterhalb des Modellperimeters mit Blick gegen die Fliessrichtung.
Der sichtbare Abfluss stammt aus der Grossen Schliere (Foto: C. Beffa)
Unterhalb der Einmündung der Grossen
Schliere wird dazu auf einer Länge von 50 m die Sohlentopographie
in einem Raster von 1
´ 2
m detailliert vermessen. Der Horizont wird mittels Baulaser definiert und
mit der Messlatte (Breite 5 cm) die Sohlenlage und die Wassertiefe bestimmt
(Abbildung 5). Bei geringerem Abfluss ist Tage zuvor die Wassertiefe mit
einem Doppelmeter (Breite 1.5 cm) aufgenommen worden. Diese Messungen werden
auf eine Lattenbreite von 5 cm umgerechnet, um einen direkten Vergleich
zu ermöglichen. Die Abflussmenge wird mit einem Messflügel ermittelt.
Der Zeitaufwand für beide Feldaufnahmen beträgt rund 16 Stunden
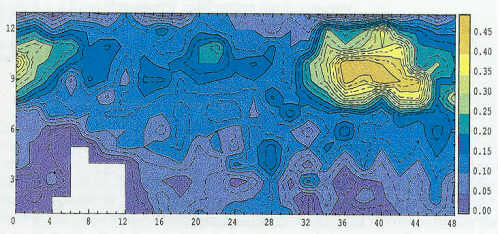
Abbildung 5: Sarner Aa: Beobachtete
Wassertiefen für den Modellperimeter bei einem Abfluss von 0.4 m3/s
(Fliessrichtung von links nach rechts; Masse in [m]). Man erkennt am rechten
Ufer eine trockene Bank und ausgangs Perimeter den Kolk als Folge der aufgerissenen
Sohlenpflästerung.
Die Erstellung des Berechnungsgitters aus
den topographischen Daten folgt dem selben Muster wie in Anwendung 1. Auch
die Sohlenrauheit wird aufgrund des mittleren Korndurchmessers bestimmt.
Die modellierten Summenhäufigkeiten für Wassertiefe und Fliessgeschwindigkeit
finden sich in Abbildung 6 dargestellt. Zur Beurteilung der Orgnismendurchgängigkeit
interessiert im weiteren die Lage des Wasserspiegels und die Wassertiefe
entlang des tiefsten Querprofilpunktes (Abbildung 7). Auch bei dieser Auswertung
stimmen Modell und Naturmessung gut überein.
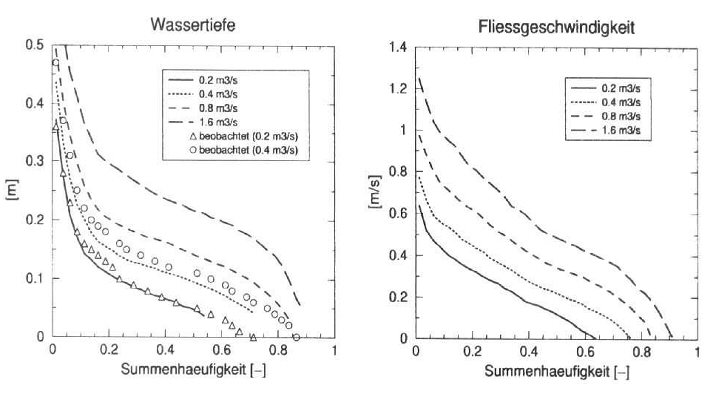
Abbildung 6: Sarner Aa: Berechnete Summenhäufigkeit
von Wassertiefe und tiefengemittelter Fliessgeschwindigkeit bei verschiedenen
Abflussmengen.
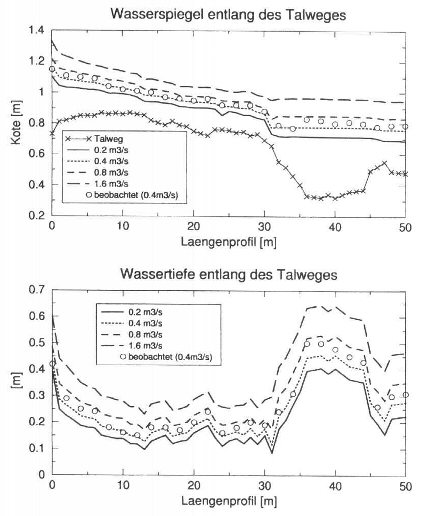
Abbildung 7: Sarner Aa: Längenprofil
von Wasserspiegel und Wassertiefe entlang des Talweges für verschiedene
Abflussmengen.
| Modellänge / -breite |
51 / 14 m
|
| Zellengrösse |
1 ´ 1 m
|
| Anzahl Zellen |
714
|
| k-Strickler-Wert |
28 m1/3/s
|
| Zuflussrand |
Normalabfluss
|
| Wegflussrand |
kritischer Abfluss
|
| Berechnungszeit pro Run (PIII, 866 MHz) |
15 s
|
Tabelle 2 - Angaben zum Modell "Sarner
Aa"
Folgerungen
Die Resultate des Modells Hydro2de
stimmen für die gezeigten Anwendungen gut bis sehr gut mit den beobachteten
Wassertiefen überein. Die Wahl der Modellparameter erfolgte dabei
ohne Kalibrierung. Damit ist eine notwendige Voraussetzung für die
Prognosefähigkeit des Modells erfüllt. Die Übereinstimmung
zwischen Modell und Natur gilt aufgrund der vorliegenden Resultate auch
für weitere Strömungsparameter wie spezifischer Abfluss, tiefengemittelte
Fliessgeschwindigkeit, Sohlenschubspannung und turbulente Energie.
Aus gewässerökologischer Sicht
stellt das Modell Hydro2de ein sehr praxistaugliches Verfahren dar.
Es vermag innert kurzer Zeit für ganze Gewässerabschnitte die
Sohlenstrukturen sowie deren hydraulischen Verhältnisse auf plausible
Art und Weise abzubilden. Es dient somit der Charakterisierung des IST-Zustandes
wie auch der Darstellung eines definierten SOLL-Zustandes, so dass daraus
nachvollziehbar Defizite abgeleitet werden können. So kann z.B. auf
einfache Art und Weise aufgezeigt werden, ab welchem Abfluss die im GSchG
(Art. 31) aufgeführte Forderung der freien Fischwanderung (nach BUWAL
2000 mindestens eine Wanderrinne von 20 cm Wassertiefe) möglich ist.
Erfahrungen aus weiteren Projekten zeigen,
dass der Einsatz eines mehrdimensionalen Modelles dort sinnvoll ist, wo
entweder die vorhandene Datengrundlage eine ausreichende Abbildung der
relevanten Sohlenstrukturen zulässt oder die Mittel für die notwendige
Datenerhebung bewilligt werden. In einem solchen Fall stellt die Modellierung
ein sehr effizientes Hilfsmittel für die Beurteilung der hydraulischen
und gewässerökologischen Verhältnisse dar. Wo diese Voraussetzungen
nicht gegeben sind, ist von einem Modelleinsatz abzuraten. Die Auftraggeber
sollten sich jedoch bewusst sein, dass damit eine Chance zur Optimierung
der Gewässerfunktionen verspielt wird.
Dank
Literatur
Beffa, C. 1994. Praktische Lösung
der tiefengemittelten Flachwassergleichungen.
VAW
Mitteilung Nr. 133,
ETH Zürich.
Beffa, C. 1996. Application of a Shallow
Water Model to Braided Flows. In: A. Müller (ed.): Proc. Hydroinformatics
´96, Zürich, 667-672.
Beffa, C. & Connell, R. 2001. "Two-Dimensional
Flood Plain Flow - Part I: Model Describtion".
Journal
of Hydrologic Engrg. ASCE, Vol. 6 No. 5, 397-405.
Bundesamt
für Wasser und Geologie (BWG) 2000. Faltblatt:
Raum den Fliessgewässern.
Bundesamt
für Umwelt, Wald und Landschaft (BUWAL) 2000. Wegleitung: Angemessene
Restwassermengen - Wie können sie bestimmt werden? BUWAL Dokumentation,
3003 Bern. Bestellnummer VU-2701-D.
Connell, R., Painter, D. & Beffa, C.
2001. "Two-Dimensional Flood Plain Flow - Part II: Model Validation". Journal
of Hydrologic Engrg. ASCE, Vol. 6 No. 5, 406-415.
Cunge, J.A. 1998. From Hydraulics to Hydroinformatics.
In: Holz, K.P., Bechteler, W., Wang, S.S.Y. & Kawahara, M. (eds.):
Proc. Advances in Hydro-Science and -Engineering, Cottbus.
Liggett, J.A. 1994. Fluid Mechanics. McGraw-Hill,
New York.
Lindner, K. 1982. Der Strömunswiderstand
von Pflanzenbeständen. Fachbereich für Bauingenieur- und Vermessungswesen,
TU Braunschweig.
Rodi, W. 1984. Turbulence Models and their
Application in Hydraulics - a State of the Art Review (2nd ed).
IAHR, Delft.
Strickler, A. 1923. Beiträge zur Frage
der Geschwindigkeitsformel und der Rauhigkeitszahl für Ströme,
Kanäle und geschlossene Leitungen. Mitteilungen des Eidg. Amtes für
Wasserwirtschaft, Bern.
Vischer, D. & Huber, A. 1993. Wasserbau
(5. Aufl.). Springer, Berlin.
Kontaktadresse:
Cornel Beffa
Postfach 28
CH-6431 Schwyz
Tel +41 41 810 07 35
Joachim Hürlimann
AquaPlus Elber Hürlimann Niederberger
Gewerbestrasse 5a
CH-6314 Unterägeri
Tel +41 41 750 50 09







